Fama–French three-factor model

In asset pricing and portfolio management the Fama-French three factor model is a model designed by Eugene Fama and Kenneth French to describe stock returns.

The traditional asset pricing model, known formally as the Capital Asset Pricing Model, CAPM, uses only one variable, beta, to describe the returns of a portfolio or stock with the returns of the market as a whole. In contrast, the Fama–French model uses three variables. Fama and French started with the observation that two classes of stocks have tended to do better than the market as a whole: (i) small caps and (ii) stocks with a high book-to-market ratio (BtM, customarily called value stocks, contrasted with growth stocks). They then added two factors to CAPM to reflect a portfolio's exposure to these two classes:^[1]

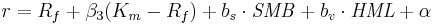
$r=R_f%2B\beta_3(K_m-R_f)%2Bb_s\cdot\mathit{SMB}%2Bb_v\cdot\mathit{HML}%2B\alpha$

Here r is the portfolio's rate of return, 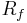$R_f$ is the risk-free return rate, and 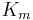$K_m$ is the return of the whole stock market. The "three factor" $\beta$ is analogous to the classical $\beta$ but not equal to it, since there are now two additional factors to do some of the work. 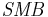$\mathit{SMB}$ stands for "small (market capitalization) minus big" and 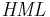$\mathit{HML}$ for "high (book-to-market ratio) minus low"; they measure the historic excess returns of small caps over big caps and of value stocks over growth stocks. These factors are calculated with combinations of portfolios composed by ranked stocks (BtM ranking, Cap ranking) and available historical market data. Historical values may be accessed on Kenneth French's web page.

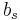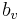Moreover, once SMB and HML are defined, the corresponding coefficients $b_s$ and $b_v$ are determined by linear regressions and can take negative values as well as positive values. The Fama-French three factor model explains over 90% of the diversified portfolios returns, compared with the average 70% given by the CAPM (within sample). The signs of the coefficients suggested that small cap and value portfolios have higher expected returns—and arguably higher expected risk—than those of large cap and growth portfolios.^[2]

Griffin shows that the Fama and French factors are country specific and concludes that the local factors provide a better explanation of time-series variation in stock returns than the global factors.^[3] Therefore, updated risk factors are available for other stock markets in the world, including United Kindom, Germany and Switzerland.

References

^ Fama, Eugene F.; French, Kenneth R. (1993). "Common Risk Factors in the Returns on Stocks and Bonds". Journal of Financial Economics 33 (1): 3–56. doi:10.1016/0304-405X(93)90023-5.
^ Fama, Eugene F.; French, Kenneth R. (1992). "The Cross-Section of Expected Stock Returns". Journal of Finance 47 (2): 427–465. doi:10.2307/2329112.
^ Griffin, John M. (2002). "Are the Fama and French Factors Global or Country Specific?". The Review of Financial Studies 15 (3): 783–803. doi:10.1093/rfs/15.3.783.
^ Carhart, Mark M. (1997). "On Persistence in Mutual Fund Performance". Journal of Finance 52 (1): 57–82. doi:10.2307/2329556.

Fama–French three-factor model

See also

References